Table of Contents
Heapsův zákon
Heapsův zákon popisuje, jak závisí přírůstek typů na přírůstku tokenů (tzv. token-type ratio, TTR). V podstatě tedy řeší úlohu tohoto typu: jak velký musíme mít korpus, pokud chceme, aby obsahoval nejméně určitý počet různých jednotek.
Obecný vzorec Heapsova zákona je:
$V(N) = a \times N^{b}$
kde N je počet tokenů a V(N) je velikost slovníku, tj. počet typů na daný počet tokenů. Koeficienty a a b jsou pro každý jazyk specifické. Koeficient b by se měl nacházet zhruba v rozsahu 0,4 < b < 0,6; koeficient a by měl být v rozsahu 10 < a < 100 (pro češtinu jsou tyto původní odhady zjevně příliš úzké).
Koeficienty pro češtinu
Pro češtinu platí zhruba tyto koeficienty:
Pro typy tvořené pomocí lemmat platí, že $a = 11.8287$ a $b = 0,5955$.
Pro typy tvořené slovními tvary má rovnice koeficienty $a = 118.0895$ a $b = 0.5113$.
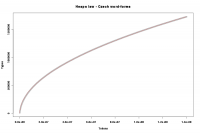
Oba modely přitom vykazují velmi malou odchylku od reality (viz detail grafu).
V praxi to znamená, že korpus, který má 120 mil. tokenů (což je případ SYN2000, SYN2005 i SYN2010 po započtení interpunkce jako samostatné pozice), by měl mít 766 tisíc různých lemmat a 1,596 mil. různých slovních tvarů (SYN2010 má 786 tisíc lemmat a 1,706 mil. tvarů - rozdíl oproti modelu je méně než 2 % a 7 %). Na druhou stranu, slovník, který by měl obsahovat 50 tisíc lemmat (což ovšem nelze ztotožňovat s 50 tisíci hesly), by se měl zakládat minimálně na korpusu o velikosti 1,227 mil. tokenů (za nesplnitelného předpokladu, že pro popis je vhodné každé lemma, třeba i vlastní jméno nebo číslo, a postačující je i jen jeden jediný výskyt lemmatu, tedy hapax; pokud bychom odhadovali počet lemmat použitelných pro slovníkový popis v každém korpusu střízlivě na 20 %, pak by bylo pro 50tisícový slovník potřeba korpus s alespoň 250 tisíci typy, což odpovídá více než 18 milionům tokenů).
Postup měření
Aby bylo vůbec možné jakkoli porovnávat výsledky měření koeficientů Heapsova zákona, je třeba se přesně držet stejného postupu. V tomto případě jsme k uvedeným výsledkům dospěli následovně:
- Korpus SYN (1,3 miliardy slov) byl rozdělen na jednotlivé opusy.
- V náhodně vybrané skupině opusů (vždy o celkové velikosti 140 milionů tokenů) byl měřen počet typů. Výpis byl prováděn vždy po 10 000 tokenech.
- Celkem bylo provedeno 100 měření na slovních tvarech a 100 měření na lemmatech. Výsledky byly zprůměrovány (aby byl eliminován vliv jednotlivých textů nebo žánrů), takže odhad je zpracován na průměrných hodnotách pro wordy a průměrných hodnotách pro lemmata.
- Model byl vytvořen v R na základě příkazu:
fit = nls(TYPES ~ I(a*TOKENS^b), data=word, start=list(a=10,b=0.5), trace=T)
Token-hapax ratio
Obdobný vztah, jako je token-type ratio (TTR), který aproximuje Heapsův zákon, je možné pozorovat i u vztahu mezi přibývajícím počtem hapaxů v závislosti na zvětšujícím se korpusu. Parametry jsou zde jiné, princip je ovšem stejný.
Analogicky k předchozímu měření můžeme i zde dospět k následujícím koeficientům pro češtinu:
Pro hapaxy tvořené lemmaty platí, že $a = 1.6935112$ (!) a $b = 0.6678874$.
Pro hapaxy tvořené slovními tvary platí, že $a = 57.28$ a $b = 0.5086$.